Deformable Kernels:
Adapting Effective Receptive Fields for
Object Deformation

Hang Gao1,3,*

Xizhou Zhu2,3,*

Steve Lin3

Jifeng Dai3

1UC Berkeley

2University of Science and Technology of China

3Microsoft Research Asia

[arXiv]

[GitHub]

How does convolutions handle object deformation? Here we show conceptually how different 3-by-3 conv kernels interact with deformations of two images. (a, b) Conventional rigid kernels cannot adapt to object deformation. (c) Previous work reconfigures data towards common arrangement to counter the effects of geometric deformation. (d) We propose to resample kernels and, in effect, adapt kernel spaces while leaving the data untouched.

Convolutional networks are not aware of an object's geometric variations, which leads to inefficient utilization of model and data capacity. To overcome this issue, recent works on deformation modeling seek to spatially reconfigure the data towards a common arrangement such that semantic recognition suffers less from deformation. This is typically done by augmenting static operators with learned free-form sampling grids in the image space, dynamically tuned to the data and task for adapting the receptive field. Yet adapting the receptive field does not quite reach the actual goal -- what really matters to the network is the *effective* receptive field (ERF), which reflects how much each pixel contributes. It is thus natural to design other approaches to adapt the ERF directly during runtime.

In this work, we instantiate one possible solution as Deformable Kernels (DKs), a family of novel and generic convolutional operators for handling object deformations by directly adapting the ERF while leaving the receptive field untouched. At the heart of our method is the ability to resample the original kernel space towards recovering the deformation of objects. This approach is justified with theoretical insights that the ERF is strictly determined by data sampling locations and kernel values. We implement DKs as generic drop-in replacements of rigid kernels and conduct a series of empirical studies whose results conform with our theories. Over several tasks and standard base models, our approach compares favorably against prior works that adapt during runtime. In addition, further experiments suggest a working mechanism orthogonal and complementary to previous works.

---

Results

What do DKs learn? We here show t-SNE results on learned control units of different operators. Qualitative, we observe that Conditional Convolutions try to gate more from semantics, while in our case, the learned kernel offsets are more scale-related.

We show learned ERFs on three images with large, medium, and small objects from the COCO test-dev split. Given each ground-truth bounding box, we visualize the non-zero ERF values of its central point. Theoretical RFs cover the whole image for all three examples and we thus ignore them in our plots. (a) Rigid kernels have strong central effects and a Gaussian-like ERF that cannot deal with object deformation alone. (b) Deformable Convolutions and (c) Deformable Kernels both tune ERFs to data. (d) Combining both operators together enables better modeling of 2D geometric transformation of objects.

---

Paper

Gao, Zhu, Lin, Dai. Deformable Kernels: Adapting Effective Receptive Fields for Object Deformation. In ICLR, 2020.

[PDF]

[Bibtex]

---

Try our code

 [PyTorch]

---

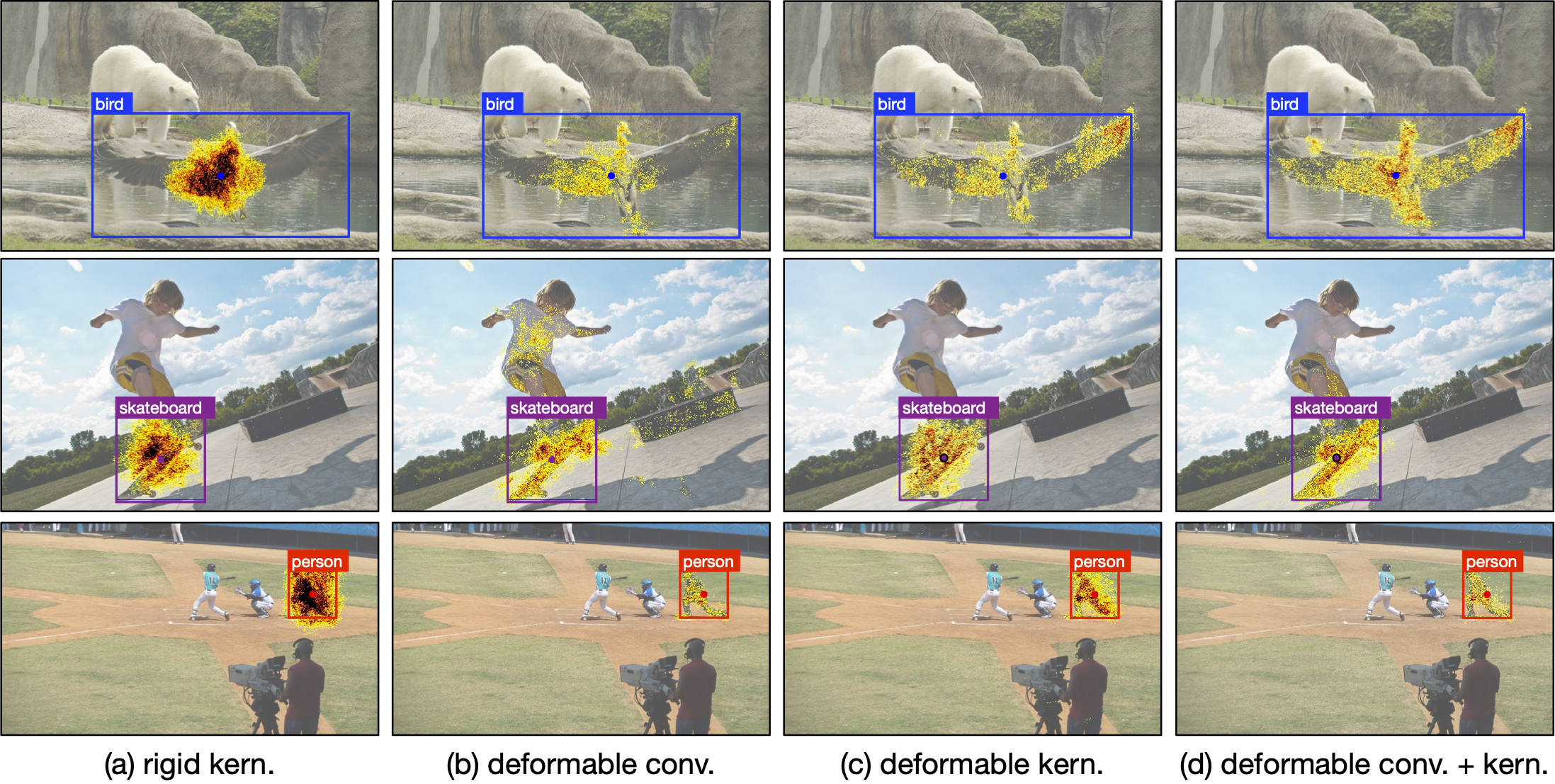
Related Work Brandon Yang, Gabriel Bender, Quoc V. Le, Jiquan Ngiam. CondConv: Conditionally Parameterized Convolutions for Efficient Inference. In NeurIPS, Apr 2019. [PDF] [GitHub] Xizhou Zhu, Han Hu, Stephen Lin, Jifeng Dai. Deformable ConvNets V2: More Deformable, Better Results. In CVPR, Nov 2018. [PDF] [GitHub] Jifeng Dai*, Haozhi Qi*, Yuwen Xiong*, Yi Li*, Guodong Zhang*, Han Hu, Yichen Wei. Deformable Convolutional Networks. In ICCV, Mar 2017. [PDF] [GitHub] Wenjie Luo*, Yujia Li*, Raquel Urtasun, Richard Zemel. Understanding the Effective Receptive Field in Deep Convolutional Neural Networks In NeurIPS, May 2016. [PDF]

---

Acknowledgements This work was done when HG and XZ were interns in Microsoft Research Asia. The webpage template was borrowed from some colorful folks .